Beware of precision without accuracy
“The test of a first-rate intelligence is the ability to hold two opposing ideas in mind at the same time and still retain the ability to function.” -F. Scott Fitzgerald
Two months ago, the most influential financial economist in history died at the age of 95. Before Harry Markowitz released his short (15-page) dryly named paper ”Portfolio Selection” (1952) for which he would later be awarded the Nobel prize in economics, there was no comprehensive theory or quantitative model for market behavior, stock pricing, risk measurement, and diversification.
In 1959. Harry’s follow-up dissertation at University of Chicago presented two huge mathematically rigorous insights: 1) an elegant relationship between stock risk and returns, and 2) a formula for evaluating portfolio diversification. For better and worse, it’s still the dominant model today.
His work, expanded greatly by other Nobel winners like William Sharpe, Eugene Fama, and Merton Miller was later dubbed Modern Portfolio Theory or (MPT). Before MPT, investors knew about risk and return and diversification only intuitively. They invested in the companies they thought had the best prospects or, with second order thinking, ones they thought other people thought had the best prospects (John Maynard Keynes’ “Beauty Contest”).
Harry simply suggested that stock risk is the propensity for the price to be low when an investor needs to sell it. In his model, risk is captured as a statistic called volatility (risk) and it could be compared directly to the stock returns (reward).
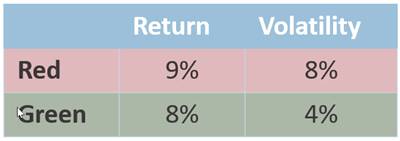
How much risk per unit of reward? is his brilliantly simple model. In the chart below, the average return of the red is higher (9%) but it’s twice as volatile.
Markowitz said rational investors should prefer the green because it had substantially less volatility with only a small trade off in return. This is one of those things that seems so obvious now that it’s hard to imagine how brilliant it is.
Harry’s second major contribution is a mathematical calculation that proves you can have higher returns or lower risk with a ”properly” diversified portfolio. It’s often called a rebalancing bonus. A quick example: from Jan 1999 to Mar 2020, two Vanguard mutual funds had the same average return of 7.10%. If you combined them together 50%/50% and rebalanced annually you get 7.86%, more than the sum of the parts. It’s a diversification benefit that has been called the only free lunch in investing. A good portfolio will optimize the potential for this benefit.
Interestingly, early reception to Harry was cold. At young Harry's PhD dissertation defense, another future Nobel laureate Milton Friedman said, ”We cannot award you with a PhD in economics for a dissertation that is not economics“. Nonetheless, within a few decades, aided by new supercomputers, MPT became the standard used by Wall Street and DC regulators.
And it still is. Wall Street worships MPT because they can sell complex-looking math and spreadsheet “solutions” that look sophisticated. Regulators bought it, believing they could “protect” consumers by ensuring these statistics were prominently displayed.
Even today, nearly three quarters of a century later, you see MPT everywhere. It’s often labeled factor investing, mean-variance, CAPM, risk-adjusted returns, and Sharpe ratio among others.
The overuse of MPT is something that has been criticized even by MPT advocates. MPT is older science. The newer behavioral school of Financial Economics has been successfully hammering away at MPT for decades, showing very serious flaws in MPT including:
It has no predictive ability. MPT is based entirely on historical data. It assumes that the future will follow the patterns of the past. We know that it probably won’t even if it’s a best guess.
Investors are not rational. MPT assumes that all investors are rational and make decisions solely on risk and return. In fact, investors often behave irrationally due to biases and psychological tendencies.
Risk is not volatility. MPT equates risk with statistical volatility and assumes a normal distribution. However, many critics say that this definition ignores other aspects of risk, such as market liquidity, systemic risk, or the risk of permanent loss.
So, what’s the answer? Modern Portfolio Theory or Behavioral Finance? If you are slavishly using MPT statistics, as many still do, you have missed the boat. MPT has huge flaws that can’t be ignored. It’s beautifully precise but still not accurate. Behavioral Finance tells us not to trust MPT but offers no alternative. The situation is not unlike the quest for a unified theory in physics. Macro-level Einstein stuff and subatomic quantum stuff both seem to be right but are theoretically unreconcilable.
Fitzgerald had a point.